Funciones

1. ¿Cómo puedes expresar la relación entre dos magnitudes como, por ejemplo, la masa y el volumen de un cuerpo?

Mediante un gráfico o una función, ya que no tienen relación entre sí. 

2. ¿Qué es una función? ¿De qué formas pueden expresarse las relaciones entre magnitudes? Pon ejemplos de funciones de la vida cotidiana; puedes buscar en revistas, periódicos, etc. En las figuras siguientes tienes 3 ejemplos: 

En matemática, una función (f) es una relación entre un conjunto dado X (llamado dominio ) y otro conjunto de elementos Y (llamado codominio ) de forma que a cada elemento x del dominio le corresponde un único elemento f(x) del codominio (los que forman el recorrido, también llamado rango o ámbito ). 

 Puede ser representadas como:

Gráfico cartesiano:

El plano cartesiano está determinado por dos rectas llamadas ejes de coordenadas:

El eje horizontal recibe el nombre de eje X o abcisas.

El eje vertical recibe el nombre Y o de ordenadas.

En ambos ejes se pueden representar los números enteros y se cruzan en el 0.

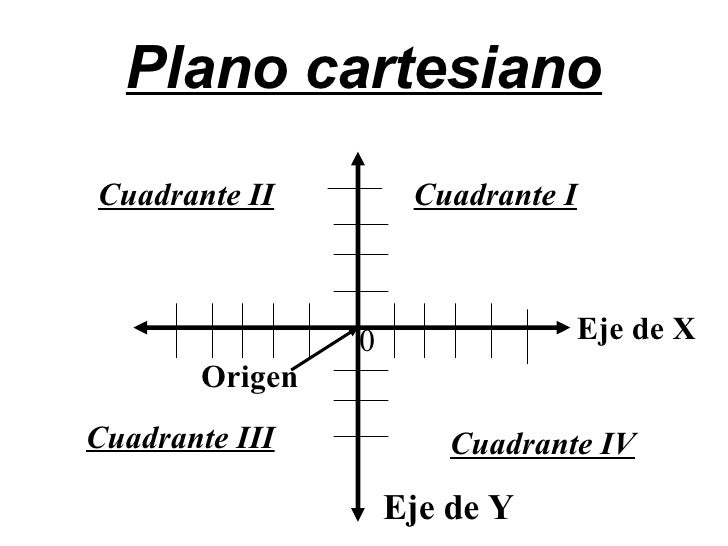
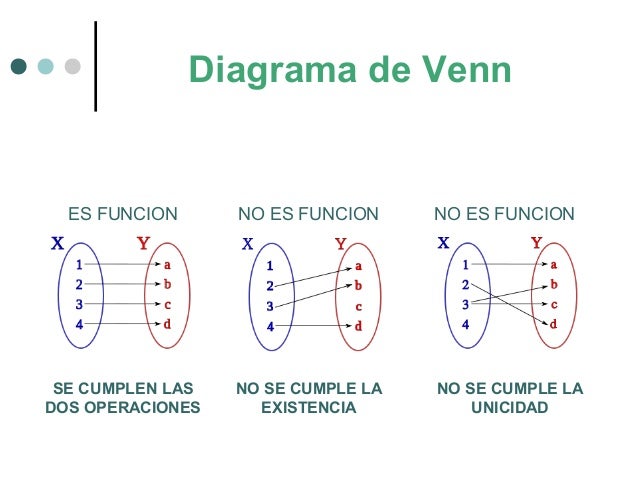
Diagrama de Venn:

Tablas

Funciones en fórmulas

Un ejemplo de una función en la vida cotidiana es por ejemplo lo que tarda la llama una vela en consumirse, el precio de un objeto, el crecimiento de las personas en la población...

Por ejemplo, el crecimiento de una flor. 

3. ¿Qué es la tasa de variación de una función? ¿Qué valores toma para las funciones crecientes y decrecientes? Puedes utilizar ejemplos gráficos para responder. 

Es la cociente entre lo que varia la `y` y lo que varia la `x` entre dos puntos de la función. 

 x : y, si el resultado es alto, significa que la función asciende muy rápido y si es bajo significa que la función asciende despacio.  Si el resultado es negativo significa que la función es descendente, y, por lo tanto, si el resultado es positivo la función asciende.

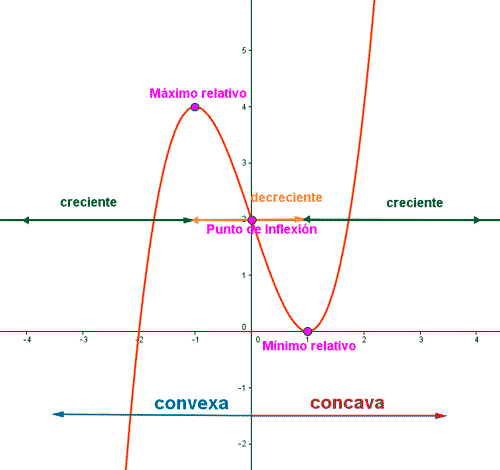
4.Utilizando la representación gráfica de una o varias funciones, explica las diferencias entre máximos y mínimos absolutos y relativos.

Los máximos y los mínimos de una función son los puntos más altos y bajos respectivamente.

• Máximo absoluto:es el punto más alto de la función.

• Mínimo absoluto:es el punto más bajo de la función.

• Máximo relativo:es el segundo punto más alto de la función.

• Mínimo relativo:es el segundo punto más bajo de la función.

5. Representa gráficamente dos ejemplos de funciones simétricas respecto al eje de ordenadas (eje y) y respecto al origen (0,0). Explica en qué consiste cada tipo de simetría.

6. Representa gráficamente una función periódica indicando por qué se denomina de esa forma.








7. Pon dos ejemplos, uno de función continua y otro de función discontinua. ¿Cuál es la diferencia entre ambas? 

8. Investiga: ¿Cuál es el origen del término función? 

El concepto de función fue usado por primera vez en 1637 por el matemático francés René Descartes para designar una potencia xn de la variable x pero en 1694 el matemático alemán Gottfried Wilhelm Leibniz utilizó el término por primera vez para referirse a varios aspectos de una curva, como su pendiente.Pero recientemente, su uso más generalizado ha sido el definido en 1829 por el matemático alemán, J.P.G. Lejeune-Dirichlet, quien definió a una variable como: Una variable es un símbolo que representa un número dentro de un conjunto de ello.

9. Representa gráficamente las funciones que se proponen indicando sus propiedades. Elabora una tabla resumen con todas las gráficas obtenidas. 

 a) Función lineal creciente ( rosa clarito )

 b) Función lineal constante (

 c) Función lineal decreciente (

 d) Rectas paralelas ( paralelas lilas )

 e) Función cuadrática cóncava (línea roja)

 f) Función cuadrática convexa (línea azul oscura)

 g) Investiga sobre la representación gráfica de otras funciones 

10. Investiga sobre la representación de funciones en coordenadas polares.

Las coordenadas polares o sistemas polares son un sistema de coordenadas bidimensional en el que cada punto del plano se determina por una distancia y un ángulo. Este sistema es ampliamente utilizado en física y trigonometría.

11.Utilizando uno de los programas anteriores investiga sobre la representación gráfica de funciones en el espacio (x, y, z).